Effect of sample timing (R example) • mipdtrial

In this vignette, we will demonstrate the following tools:

Using {mipdtrial} to simulate a trial, with the trial design specified using R code.
We will have two trial “arms”, varying only by the therapeutic drug monitoring strategy used. The two arms will be defined by two different calls to create_sampling_design()

Motivation

A hospital currently collects two samples for adjusting vancomycin doses: one at 1-hr post-dose and another at 9 hours post-dose. They want to compare the impact on target attainment (an area under the curve (AUC) of 400-600 mg*h/L) if they were to switch to collecting a single sample at 5 hours post-dose.

Here is how we could answer that problem using simulation!

library(mipdtrial)
library(dplyr)   # for easier data manipulation 
library(tidyr)
library(ggplot2) # for plotting our results
if(!requireNamespace("pkvancothomson", quietly = TRUE)) {
  PKPDsim::install_default_literature_model("pk_vanco_thomson")
  loadNamespace("pkvancothomson")
}

1. Define trial design

This simulated trial will have two arms:

Two samples, collected 1 and 9 hours after a dose
One sample, collected 5 hours after a dose

In each case, we will collect the samples in the fourth dosing interval, and for simplicity, we will assume all patients are receiving vancomycin twice daily, infused over 2 hours.

tdm_design1 <- create_sampling_design(
  offset = c(1, 9),
  at = c(4, 4), 
  anchor = "dose"
)
tdm_design2 <- create_sampling_design(
  offset = 5,
  at = 4,
  anchor = "dose"
)

We will adjust the fifth dose based on these levels, aiming for a daily AUC of 400-600 mg*h/L by day 6. We will use the Thomson (2009) model for simulating patient pharmacokinetics.

update_design <- create_regimen_update_design(
  at = 5,
  anchor = "dose",
  dose_optimization_method = map_adjust_dose
)
target_design <- create_target_design(
  targettype = "auc24", 
  targetmin = 400,
  targetmax = 600,
  at = 6,
  anchor = "day"
)
model_design <- create_model_design(lib = "pkvancothomson")

Our initial dosing strategy will be based on population PK parameters, with dose size calculated to reach the specified target for a dosing interval of 12 hours.

initial_method <- create_initial_regimen_design(
  method = model_based_starting_dose,
  regimen = list(
    interval = 12,
    type = "infusion",
    t_inf = 1
  ),
  settings = list(
    auc_comp = 3,
    dose_resolution = 250,
    dose_grid = c(250, 5000, 250)
  )
)

Now we can combine all these design choices together:

design1 <- create_trial_design(
  sampling_design = tdm_design1, # arm 1
  target_design = target_design,
  regimen_update_design = update_design,
  initial_regimen_design = initial_method,
  sim_design = model_design, est_design = model_design
)

design2 <- create_trial_design(
  sampling_design = tdm_design2, # arm 2
  target_design = target_design,
  regimen_update_design = update_design,
  initial_regimen_design = initial_method,
  sim_design = model_design, est_design = model_design
)

2. Create a set of digital patient covariates

For this example, we will randomly generate a set of weights and creatinine clearances (CRCLs) for our synthetic data set.

set.seed(15)
dat <- data.frame(
  ID = 1:30,
  weight = rnorm(30, 90, 25),               # kg, normally distributed
  crcl = exp(rnorm(30, log(6), log(1.6)))   # L/hr, log-normally distributed 
)

We will use the Thomson (2009) model, which accepts additional clearance from hemodialysis as a covariate. Let’s set that to zero in our data set.

Other models might require fat-free mass or other calculated covariates. This would be a good time to do that sort of processing on your data set!

dat$CL_HEMO <- 0

Here are the first few rows of our data set:

head(dat)
#>   ID    weight      crcl CL_HEMO
#> 1  1  96.47057  4.827349       0
#> 2  2 135.77802  6.013269       0
#> 3  3  81.50954 11.863322       0
#> 4  4 112.42995  8.546496       0
#> 5  5 102.20041  9.448520       0
#> 6  6  58.61535  7.477850       0

We also need to link the covariates in our data set to the covariates expected in the model:

To check which covariates are required for your model use PKPDsim::get_model_covariates():
```
PKPDsim::get_model_covariates(model_design$model)
#> [1] "WT"      "CRCL"    "CL_HEMO"
```

To check which covariates are in your data set use colnames():

colnames(dat)
#> [1] "ID"      "weight"  "crcl"    "CL_HEMO"

cov_map <- c(
  WT = "weight", 
  CRCL = "crcl",
  CL_HEMO = "CL_HEMO"
)

3. Simulate a trial!

Patients will get a model-based dose (using population PK parameters), and then this dose will be adjusted based on the MAP Bayesian fit made using the collected samples.

Individual PK parameters will be randomly generated based on the interindividual variability described in the model, and residual variability will be added to each sample collected using the error model described in the model.

res1 <- run_trial(data = dat, design = design1, cov_mapping = cov_map, seed = 15)
#> ================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================
res2 <- run_trial(data = dat, design = design2, cov_mapping = cov_map, seed = 15)
#> ================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

We can look at final exposure estimates for each arm:

final_exp1 <- res1$final_exposure %>%
  mutate(arm = "peak-trough")
final_exp2 <- res2$final_exposure %>%
  mutate(arm = "mid-interval")
results <- bind_rows(final_exp1, final_exp2)
head(results)
#>   id auc_true  auc_est         arm
#> 1  1 531.2769 499.9513 peak-trough
#> 2  2 499.4509 500.0458 peak-trough
#> 3  3 318.2776 499.9952 peak-trough
#> 4  4 664.3875 500.0520 peak-trough
#> 5  5 384.5240 500.0313 peak-trough
#> 6  6 590.1372 500.0520 peak-trough

4. Analyze results

We are interested in AUC target attainment. How did target attainment compare between the two arms of the trial?

target_attainment <- results %>%
  mutate(ontarget = ifelse(auc_true >= 400 & auc_true <= 600, 1, 0)) %>%
  group_by(arm) %>%
  summarize(prop_on_target = 100 * mean(ontarget))
target_attainment %>%
  ggplot() +
    aes(x = arm, y = prop_on_target) +
    geom_bar(stat = "identity") +
    theme_minimal() +
    theme(
      panel.grid.major.x = element_blank()
    ) +
    labs(
      x = "Sampling strategy",
      y = "Percent on target (%)"
    )

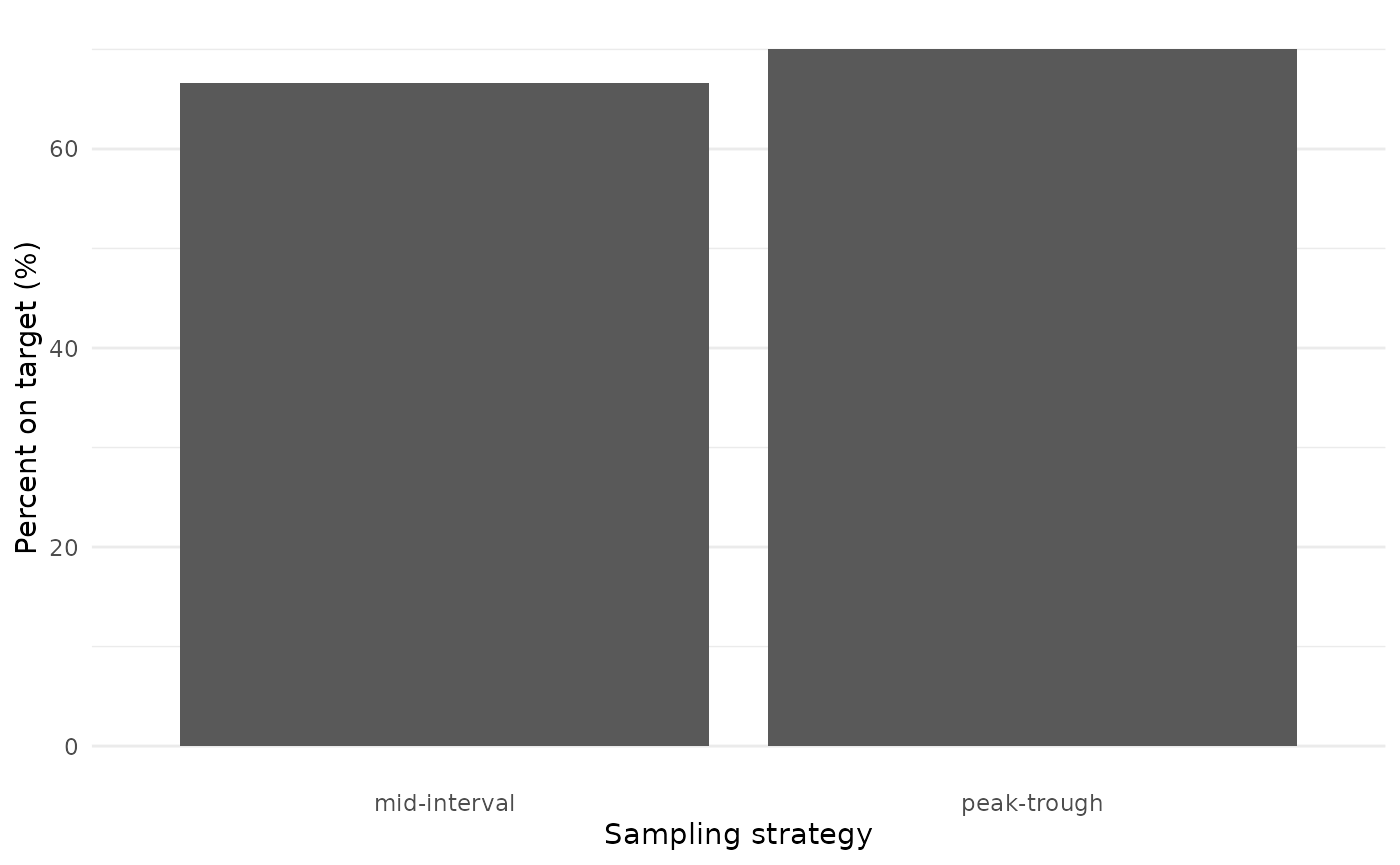
Target attainment was high and varied little between the two arms, providing evidence to support the move from collecting two samples to collecting a single sample per dosing interval.

Because we are simulating each sampling strategy in each patient, we can also look at how each patient responded to each sampling strategy.

results %>%
  select(id, auc_true, arm) %>%
  pivot_wider(names_from = arm, values_from = auc_true) %>%
  ggplot() +
    aes(x = `peak-trough`, y = `mid-interval`) +
    geom_rect(
      aes(xmin = 400, xmax = 600, ymin = -Inf, ymax = Inf), 
      fill = "grey70",
      alpha = 0.05
    ) +
    geom_rect(
      aes(ymin = 400, ymax = 600, xmin = -Inf, xmax = Inf),
      fill = "grey70",
      alpha = 0.05
    ) +
    geom_point() +
    theme_minimal()

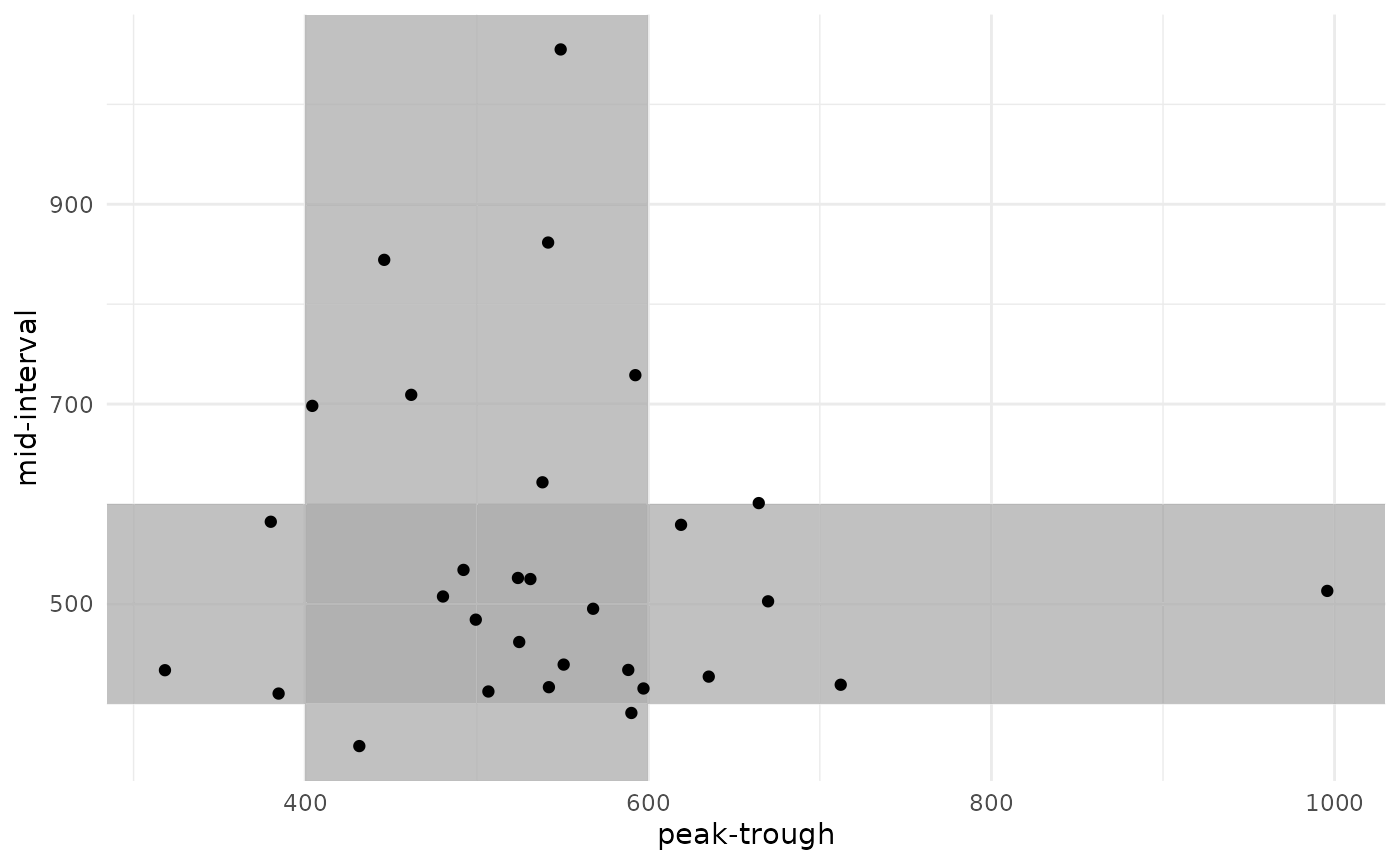
There is a strong correlation in final AUC between the two sampling strategies. Some patients were under-exposed or over-exposed in both strategies, while others were on-target in one strategy but not in the other.